Design#
pysatl-mpest — это Python-библиотека, предназначенная для оценки параметров смесей вероятностных распределений.
Ключевой особенностью библиотеки является гибкая и расширяемая архитектура, позволяющая пользователям конструировать итеративные алгоритмы оценки путем комбинирования различных шагов (например, шагов максимизации, вычисления моментов и т.д.).
На данный момент система позволяет:
Описывать непрерывные распределения и их смеси, а так же работать с ними как с объектами теории вероятностей (Готово)
Выполнять предобработку данных:
Оценивать количество компонент (В разработке)
Проводить инициализацию начального приближения путем кластеризации (В разработке)
Конфигурировать и запускать сложные итеративные алгоритмы оценки параметров смеси:
Комбинировать различные шаги алгоритма, например E шаг + LMoments шаг или E шаг + ВашЭкзотическийШаг (Готово)
Настраивать условие остановки алгоритма (Готово)
Настраивать удаление лишних компонент (Готово)
Для удобства API система предоставляет “Фасады”, с помощью которых можно легко сконфигурировать типовые алгоритмы, например EM или ELM алгоритмы. (В разработке)
Запускать “прямые” неитеративные алгоритмы оценки параметров смеси. (В разработке)
В дальнейшем планируется поддержка:
Дискретных и многомерных распределения
Поддержка большего числа алгоритмов.
Реализация бенчмаркинга и его внедрение в
pysatl-experiment.
Глоссарий#
Плотность распределения#
Представьте, что вы стреляете в мишень. Плотность вероятности в данном случае — это функция, которая описывает, в какие области мишени вы попадаете чаще всего. Там, где плотность выше, — там больше попаданий. Аналогично, для любой случайной величины, будь то рост человека или время ожидания автобуса, плотность вероятности показывает, какие значения являются более вероятными. Геометрически, вероятность того, что случайная величина примет значение из некоторого интервала, равна площади под графиком плотности на этом интервале.
Введём формальное определение:
Пусть \((\mathcal{X}, \mathcal{A},P)\) \(-\) вероятностное пространство, \(\mathcal{X} \subseteq \mathbb{R}\). Случайная величина \(X\) называется абсолютно непрерывной, если существует такая неотрицательная интегрируемая по Лебегу функция \(f: \mathcal{X} \to \mathbb{R}_{\ge 0}\) называемая плотностью вероятности, если для любого борелевского множества \(A \in \mathcal{A}\) выполняется:
Функция плотности \(f(x)\) должна удовлетворять следующим свойствам:
Неотрицательность: \(f(x) \ge 0, ~ \forall x \in \mathcal{X}\)
Нормировка: \(\int_{\mathcal{X}} f(x)dx = 1\)
Под борелевским множеством мы подразумеваем “хорошие множества”, например интервал \([-1, 1]\)
Смесь распределений#
Часто данные, с которыми мы работаем, неоднородны. Они могут происходить из нескольких скрытых, или латентных, подгрупп. Представьте, что вы анализируете данные о росте взрослых людей в городе. Скорее всего, вы заметите, что распределение роста имеет не один пик, а два: один соответствует среднему росту женщин, а другой — мужчин. Описать такие данные одной простой функцией плотности (например, одним нормальным распределением) будет некорректно. Гораздо естественнее смоделировать их как смесь двух нормальных распределений, где каждое распределение описывает свою подгруппу, а их веса в смеси отражают долю каждой подгруппы в общей популяции.
Формально, смесь вероятностных распределений — это вероятностное распределение, плотность которого является взвешенной суммой плотностей других распределений (компонент). Плотность смеси задается следующим образом:
где:
\(n\) \(-\) количество компонент смеси.
\(F = \{f_1, \dots, f_n \}\) \(-\) множество плотностей компонент. Каждая компонента принадлежит определенному параметрическому семейству распределений (например, семейству нормальных или экспоненциальных распределений).
\(\Theta = \{\Theta_1, \dots, \Theta_n\}\) \(-\) множество допустимых параметров компонент, то есть \(\Theta_k\) означает, что для \(k\)-ой компоненты параметр \(\theta_k \in \Theta_k\).
\(\Omega = \{\omega_1, \dots, \omega_n \}\) \(-\) множество весов компонент, удовлетворяющих условиям:
Неотрицательность: \(\omega_k \ge 0 ~~~\forall k\)
Нормировка: \(\sum_{k=1}^n \omega_k = 1\), для того, чтобы итоговая функция плотности \(f(x ~|~ F, \Theta, \Omega)\) была корректной.
Пример плотности смеси распределений с двумя нормальными компонентами:
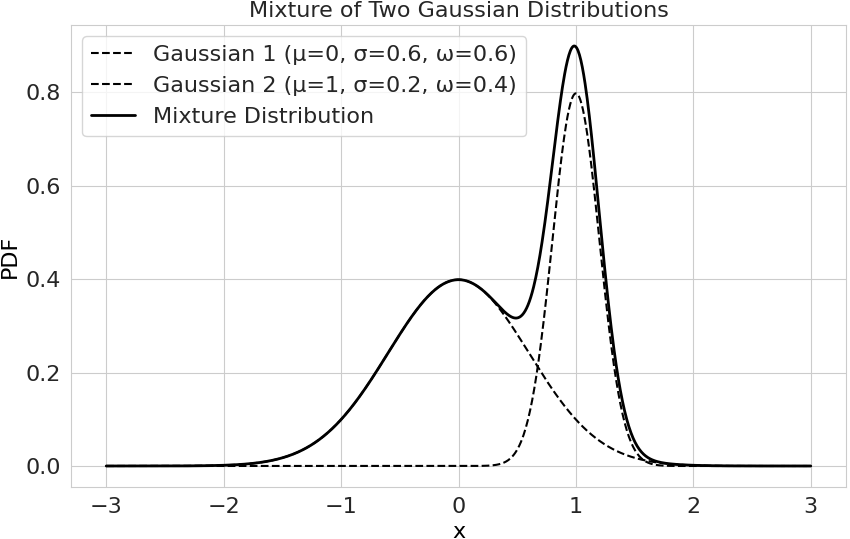
Выборка#
Представьте, что вы хотите узнать средний рост всех жителей города. Эта гипотетическая полная совокупность всех жителей называется генеральной совокупностью. Опросить абсолютно каждого человека практически невозможно. Вместо этого вы измеряете рост, скажем, 1000 случайно выбранных людей. Этот набор из 1000 измерений и есть выборка. Основная идея статистики заключается в том, чтобы по свойствам этой выборки (например, по среднему росту в ней) сделать обоснованные выводы о свойствах всей генеральной совокупности.
В контексте анализа данных, выборка — это тот набор данных, который у вас есть на руках (например, файл с измерениями), и на основе которого вы будете строить и оценивать модель.
Формально, случайная выборка объема \(n\) из распределения с плотностью \(f(x~|~\theta)\) \(-\) это набор из \(n\) случайных величин \(\{X_1, \dots, X_n\}\) удовлетворяющий следующим условиям:
Независимость: Результат одного наблюдения не влияет на результаты других. (Значение роста одного случайно выбранного человека не зависит от роста другого).
Одинаковая распределённость: Все наблюдения \(X_i\) подчиняются одному и тому же закону распределения с плотностью \(f(x ~|~ \theta)\).
Такое предположение часто называют \(i.i.d\), будем писать что данные \(X\) подчиняются закону распределения (например нормальному с параметрами \(\mu, \sigma^2\)) так:
На практике под выборкой чаще всего понимают реализацию этих случайных величин — то есть конкретный набор наблюдаемых числовых данных \(\{x_1, \dots, x_n\}\), который используется для оценки неизвестных параметров модели. Именно такая выборка передаётся в оценщики библиотеки pysatl-mpest.
Функция правдоподобия#
Представьте, что вы нашли на земле монету и хотите понять, является ли она “честной”. Вы подбрасываете ее 100 раз и получаете результат: 70 орлов и 30 решек. Возникает вопрос: какая степень “нечестности” монеты лучше всего объясняет такой исход?
Функция правдоподобия как раз и отвечает на этот вопрос. Она переворачивает стандартную логику вероятности. Вместо того чтобы, зная параметры модели (например, вероятность выпадения орла \(p = 0.5\)) предсказывать исход, мы, наоборот, используем уже наблюдаемый исход (70 орлов, 30 решек), чтобы оценить, какие параметры модели (\(p\)) являются наиболее “правдоподобными”.
Формально, пусть \(X \overset{i.i.d}{\sim} f(x~|~\theta)\). Тогда функцией правдоподобия называется функция от параметра \(\theta\), рассматриваемая при фиксированных данных \(X\):
На практике мы будем работать с логарифмом функции правдоподобия: \(\log \mathcal{L}(\theta ~|~ x_1, \dots,x_n)\ \), поскольку тогда мы будем работать не с произведением, а с суммой.
Q-функция#
Представим нашу задачу с ростом людей, который мы моделируем как смесь двух нормальных распределений (мужчин и женщин). Если бы для каждого человека в выборке мы бы точно знали, к какой группе он относится (мужчина или женщина), задача оценки была бы простой: мы бы разделили данные на две группы и оценили параметры для каждой отдельно.
Но у нас нет этой информации — принадлежность к группе является скрытой (латентной) переменной. Алгоритм EM (Expectation-Maximization), центральной частью которого является Q-функция, элегантно решает эту проблему.
Идея EM-алгоритма в следующем:
E-шаг (Expectation): Имея текущие оценки параметров (например, средний рост и дисперсию для мужчин и женщин), мы вычисляем вероятностную принадлежность каждого наблюдения к каждой компоненте. Например, для человека ростом 175 см мы можем вычислить, что он с вероятностью 70% относится к группе мужчин и с 30% — к группе женщин.
M-шаг (Maximization): Мы хотим обновить параметры модели. Но как это сделать, если принадлежность нечеткая? Здесь и появляется Q-функция. Она представляет собой “ожидаемое” значение логарифма правдоподобия, если бы мы знали скрытые переменные. Это ожидание вычисляется с использованием тех самых вероятностей, которые мы получили на E-шаге.
Проще говоря, Q-функция — это суррогатная, более простая функция, которую мы максимизируем на M-шаге вместо истинного, но слишком сложного логарифма правдоподобия.
Более формально, пусть:
\(X\) \(-\) наблюдаемые данные.
\(Z\) \(-\) скрытые переменные.
\(\Omega^{(t)}, \Theta^{(t)}\) \(-\) параметры смеси на шаге \(t\).
Тогда Q-функция определяется как условное математическое ожидание логарифма правдоподобия полных данных:
Технологический стек#
Язык: Python 3.11+
Основные библиотеки:
numpy: для всех численных вычислений и работы с многомерными массивами (ndarray).scipy: для численных методов (оптимизация, решение систем уравнений, нахождение нулей функции).sklearn: для кластеризации.pytest + pytest-mock + hypothesis: фреймворки для тестирования.sphinx: для генерации документации.