Дерево алгоритмов

Основным понятием, являющимся центром всей архитектуры модуля алгоритмов, является “дерево алгоритмов”, показывающее то, как система выполняет пошаговый процесс оценки параметров: от предварительной настройки до выбора и выполнения одного из доступных семейств алгоритмов.

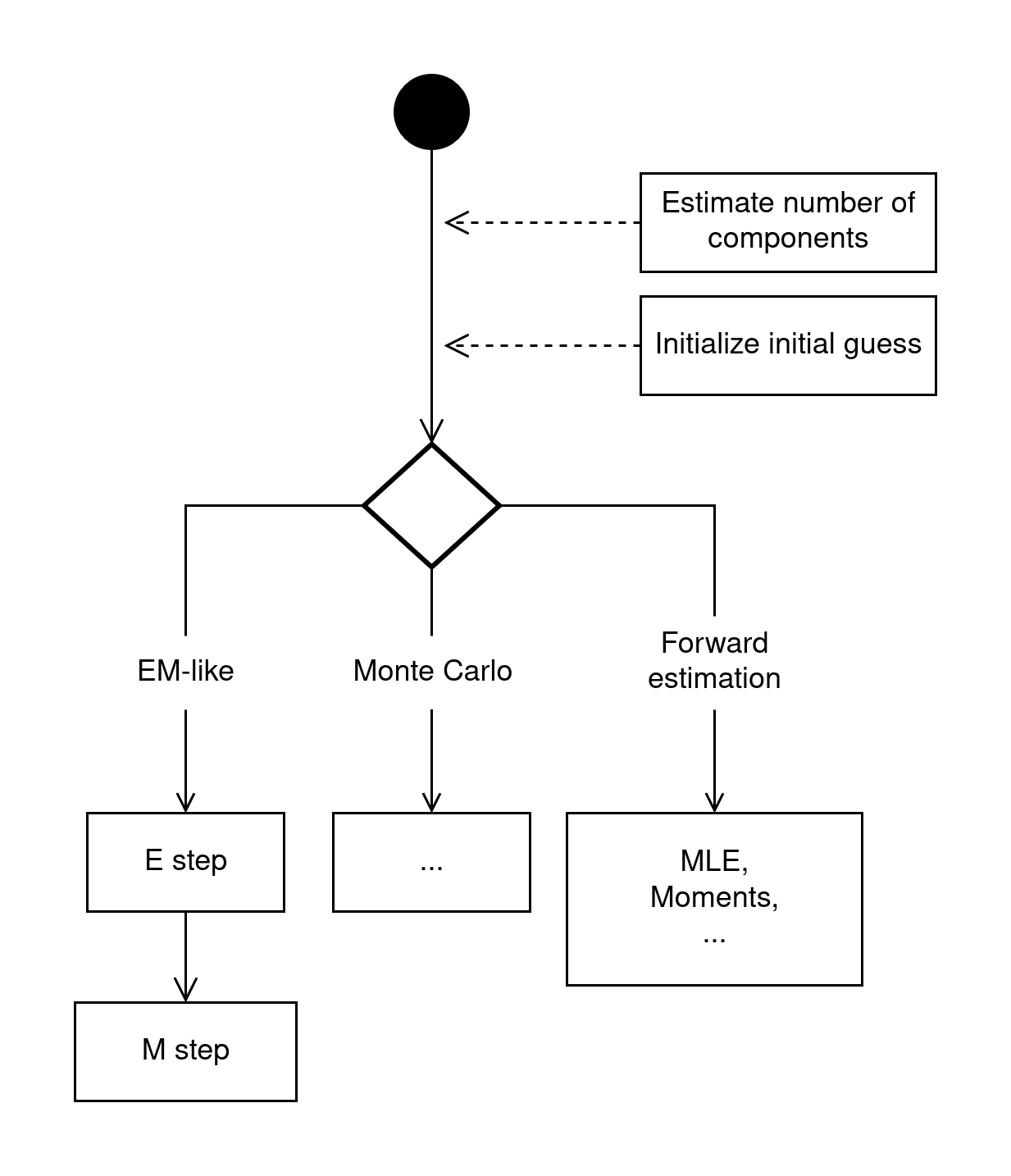
Процесс можно разбить на следующие логические этапы:

1. Начало и предварительная настройка:

   • Процесс начинается с получения входных данных (выборка, для которой мы хотим оценить смесь).

   • Перед запуском основного алгоритма выполняются два ключевых подготовительных шага, которые предоставляют начальные условия:

     • Estimate number of components (Оценка числа компонент): Определение предполагаемого количества компонент в смеси.

     • Initialize initial guess (Инициализация начального приближения): Задание стартовых значений параметров для алгоритмов.

2. Выбор семейства алгоритмов (Точка ветвления):

   • На основе конфигурации или выбора пользователя, система переходит к одному из трех основных семейств алгоритмов (обозначено ромбом). Это ключевая точка, обеспечивающая гибкость системы.

3. Исполнение алгоритма:

   • Ветвь EM-like (EM-подобные алгоритмы):

     • Представляет итеративные алгоритмы, основанные на максимизации ожидания.

     • Классический цикл состоит из двух шагов: E-step (Expectation) и M-step (Maximization), которые повторяются до сходимости.

   • Ветвь Monte Carlo (Методы Монте-Карло):

     • Представляет алгоритмы, основанные на стохастическом сэмплировании (например, MCMC).

     • Внутренняя структура этих методов пока что не рассматривается и здесь обозначена многоточием (…)

   • Ветвь Forward estimation (Прямое оценивание):

     • Представляет неитеративные методы.

     • Примерами таких методов являются MLE и Метод моментов.

EM-like

Как было показано в общей архитектуре “дерева алгоритмов”, одной из ключевых стратегий оценки является EM-like. Данная диаграмма детализирует внутреннюю структуру этого итеративного процесса.

Процесс состоит из двух фундаментальных шагов, выполняемых последовательно в цикле: E-step (шаг ожидания) и M-step (шаг максимизации):

1. E-step (Шаг ожидания):

   • Вход: На вход шага поступает текущее состояние модели смеси (Mixture).

   • Задача: Основная задача этого шага — вычислить “ответственность” (responsibilities) каждой компоненты смеси за каждую точку данных. По сути, это оценка скрытых (latent) переменных — вероятностей того, что \(i\)-ая точка данных принадлежит \(k\)-ой компоненте.

   • Выход: Результатом являются вычисленные “ответственности”, которые вместе с исходными данными передаются на следующий шаг.

2. M-step (Шаг максимизации):

   • Вход: На вход поступают данные и вычисленные на E-шаге “ответственности”.

   • Задача: Цель этого шага — обновить параметры \(\Theta, \Omega\) модели смеси.

   • Архитектурная особенность: параметры компонент оцениваются независимо и параллельно. Для каждой компоненты можно указать собственные оценки стратегий а так же выбрать параметры, которые будут оценены. Таким образом можно для некоторых компонент оценить сначала один параметр, потом другой.

   • Доступные стратегии:

     • Q-function

     • Moments

     • L-moments

     • TL-moments

     • LQ-moments

3. Завершение итерации:

   • Выход: На выходе M-шага мы получаем обновленную модель смеси (Mixture).

   • Эта обновленная модель затем используется как входная для следующей итерации E-шага. Цикл “E-step -> M-step” повторяется до тех пор, пока не будет достигнут критерий останова. В конце каждой итерации происходит “pruning” смеси, отсекая ненужные компоненты (например те, которые вносят почти нулевой вклад в смесь).

Monte Carlo

Пока что не рассматривались.

Forward estimation

Эта ветвь объединяет неитеративные методы оценки параметров смеси. В отличие от EM-алгоритмов, которые уточняют параметры шаг за шагом, методы прямого оценивания вычисляют их напрямую на основе свойств выборки.

Основными представителями этого семейства являются Метод Максимального Правдоподобия (MLE) и Метод Моментов (Method of Moments).

Метод Максимального Правдоподобия (MLE)

Идея: Метод заключается в поиске таких параметров модели (\(\Theta\) и \(\Omega\)), при которых наблюдаемые данные являются наиболее “вероятными”.

Процесс:

1. Формирование функции правдоподобия: Для смеси распределений функция правдоподобия \(L(\Theta, \Omega~|~ x)\) строится на основе функции плотности \(f(x ~|~ \Theta, \Omega)\).

2. Максимизация: Находится максимум логарифма этой функции.

Метод Моментов (MoM)

Пока что не рассматривался.